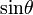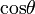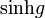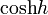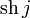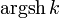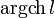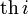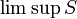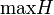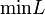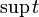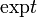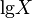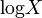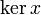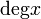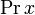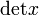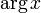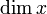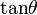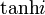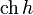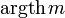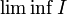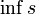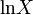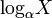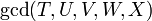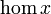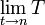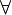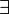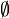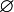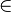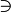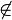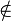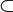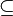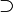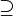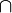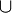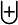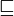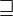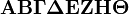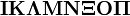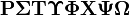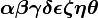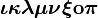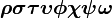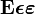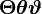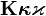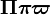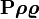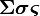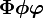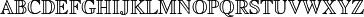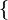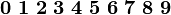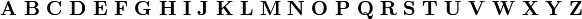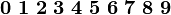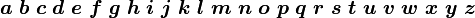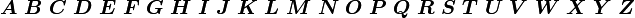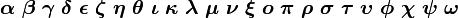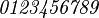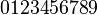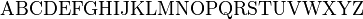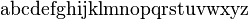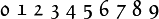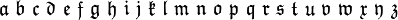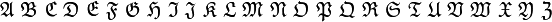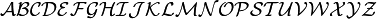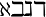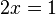根据左侧文章目录,快速定位想要的符号
声调
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| bar{x} |
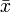 |
acute{eta} |
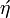 |
check{alpha} |
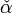 |
| grave{eta} |
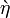 |
breve{a} |
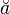 |
ddot{y} |
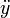 |
| dot{x} |
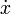 |
hat{alpha} |
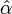 |
tilde{iota} |
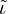 |
函数
| 语法 |
效果 |
语法 |
效果 |
| sintheta |
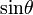 |
costheta |
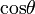 |
| arcsinfrac{L}{r} |
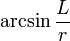 |
arccosfrac{T}{r} |
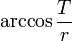 |
| sinh g |
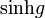 |
cosh h |
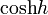 |
| operatorname{sh}j |
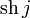 |
operatorname{argsh}k |
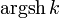 |
| operatorname{argch}l |
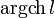 |
operatorname{th}i |
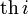 |
| k’(x)=lim_{Delta xto 0}frac{k(x)-k(x-Delta x)}{Deltax} |
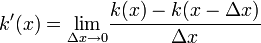 |
limsup S |
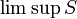 |
| max H |
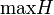 |
min L |
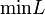 |
| sup t |
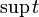 |
exp!t |
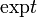 |
| lg X |
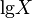 |
log X |
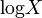 |
| ker x |
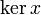 |
deg x |
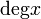 |
| Pr x |
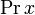 |
det x |
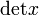 |
| arg x |
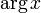 |
dim x |
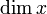 |
| tantheta |
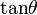 |
arctanfrac{L}{T} |
 |
| tanh i |
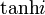 |
operatorname{ch}h |
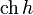 |
| operatorname{argth}m |
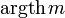 |
liminf I |
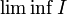 |
| inf s |
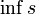 |
ln X |
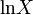 |
| log_alpha X |
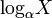 |
gcd(T,U,V,W,X) |
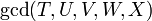 |
| hom x |
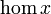 |
lim_{tto n}T |
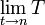 |
同余
| 语法 |
效果 |
语法 |
效果 |
| pmod{m} |
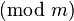 |
a bmod b |
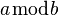 |
微分
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| nabla |
 |
partial x |
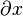 |
mathrm{d}x |
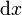 |
| dot x |
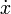 |
ddot y |
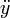 |
|
|
集合
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| forall |
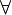 |
exists |
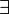 |
empty |
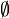 |
emptyset |
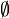 |
varnothing |
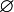 |
| in |
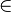 |
ni |
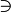 |
notin |
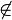 |
notin |
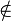 |
subset |
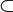 |
| subseteq |
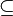 |
supset |
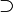 |
supseteq |
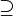 |
cap |
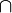 |
bigcap |
 |
| cup |
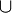 |
bigcup |
 |
biguplus |
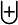 |
sqsubset |
 |
sqsubseteq |
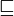 |
| sqsupset |
 |
sqsupseteq |
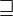 |
sqcap |
 |
sqcup |
 |
bigsqcup |
 |
逻辑
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| p |
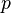 |
land |
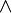 |
wedge |
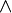 |
bigwedge |
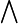 |
| bar{q} to p |
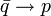 |
lor |
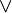 |
vee |
 |
bigvee |
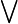 |
| lnot |
 |
neg q |
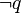 |
setminus |
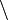 |
smallsetminus |
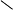 |
根号
| 语法 |
效果 |
语法 |
效果 |
| sqrt{3} |
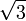 |
sqrt[n]{3} |
![pagecolor{White}sqrt[n]{3}](/wp-content/uploads/replace/21cb8585a0a0b036ee2109bb1d68eb1e.png) |
关系符号
| 语法 |
效果 |
Delta ABCsimDelta XYZ |
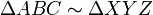 |
sqrt{3}approx1.732050808ldots |
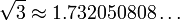 |
| simeq |
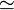 |
| cong |
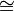 |
| dot= |
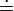 |
ggg |
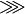 |
gg |
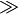 |
> |
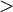 |
ge |
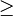 |
geqq |
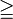 |
= |
 |
leq |
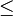 |
leqq |
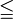 |
< |
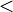 |
ll |
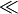 |
lll |
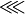 |
(x-y)^2equiv(-x+y)^2equiv x^2-2xy+y^2 |
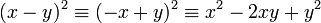 |
| xnotequiv N |
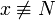 |
| xne A |
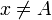 |
| xneq C |
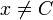 |
| tpropto v |
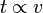 |
| pm |
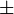 |
| mp |
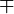 |
因为所以
begin{align}
because
begin{cases}
acute{a}x^2+bx^2+cgtrless0gtrlessgrave{a}x^2+bx^2+c
acute{a}>0>grave{a}
end{cases}
therefore
frac{-bpmsqrt{b^2-4acute{a}c}}{2acute{a}}{}_lessgtr^gtrlessx_lessgtr^gtrlessfrac{-bpmsqrt{b^2-4grave{a}c}}{2grave{a}}
end{align}
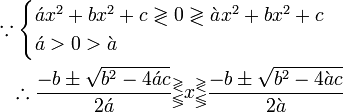
几何符号
| 特征 |
语法 |
效果 |
|
| 菱形 |
Diamond |
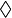 |
|
| 正方形 |
Box |
 |
|
| 三角形 |
Delta |
Delta |
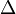 |
| 图型 |
triangle |
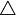 |
|
| 角名 |
angleAlphaBetaGamma |
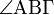 |
|
| 角度 |
sin!frac{pi}{3}=sin60^operatorname{omicron}=frac{sqrt{3}}{2} |
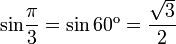 |
|
| 垂直 |
perp |
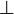 |
|
箭头符号
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| leftarrow |
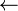 |
gets |
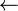 |
rightarrow |
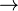 |
| to |
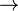 |
leftrightarrow |
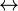 |
longleftarrow |
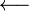 |
| longrightarrow |
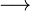 |
mapsto |
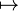 |
longmapsto |
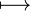 |
| hookrightarrow |
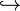 |
hookleftarrow |
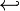 |
nearrow |
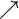 |
| searrow |
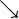 |
swarrow |
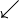 |
nwarrow |
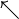 |
| uparrow |
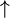 |
downarrow |
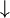 |
updownarrow |
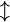 |
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| rightharpoonup |
 |
rightharpoondown |
 |
leftharpoonup |
 |
leftharpoondown |
 |
| upharpoonleft |
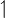 |
upharpoonright |
 |
downharpoonleft |
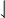 |
downharpoonright |
 |
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| Leftarrow |
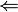 |
Rightarrow |
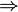 |
Leftrightarrow |
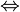 |
| Longleftarrow |
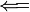 |
Longrightarrow |
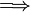 |
Longleftrightarrow (or iff) |
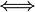 |
| Uparrow |
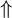 |
Downarrow |
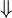 |
Updownarrow |
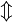 |
特殊符号
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| eth |
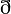 |
S |
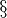 |
P |
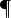 |
% |
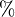 |
dagger |
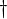 |
ddagger |
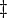 |
| star |
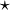 |
* |
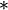 |
ldots |
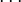 |
smile |
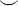 |
frown |
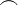 |
wr |
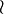 |
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| oplus |
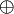 |
bigoplus |
 |
otimes |
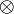 |
| bigotimes |
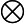 |
times |
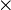 |
cdot |
 |
| div |
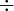 |
circ |
 |
bullet |
 |
| bigodot |
 |
boxtimes |
 |
boxplus |
 |
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| triangleleft |
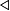 |
triangleright |
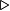 |
infty |
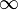 |
bot |
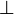 |
| top |
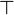 |
vdash |
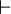 |
vDash |
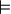 |
Vdash |
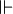 |
| models |
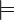 |
lVert |
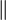 |
rVert |
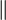 |
|
|
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| imath |
 |
hbar |
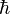 |
ell |
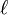 |
| mho |
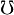 |
Finv |
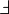 |
Re |
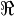 |
| Im |
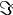 |
wp |
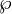 |
complement |
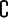 |
| 语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
语法 |
效果 |
| diamondsuit |
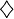 |
heartsuit |
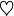 |
clubsuit |
 |
spadesuit |
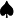 |
| Game |
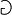 |
flat |
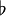 |
natural |
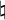 |
sharp |
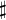 |
分数、矩阵和多行列式

上标、下标及积分等
| 功能 |
语法 |
效果 |
| 上标 |
a^2 |
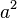 |
| 下标 |
a_2 |
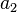 |
| 组合 |
a^{2+2} |
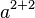 |
a_{i,j} |
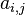 |
|
| 结合上下标 |
x_2^3 |
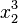 |
| 前置上下标 |
{}_1^2!X_3^4 |
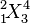 |
| 导数(HTML) |
x' |
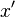 |
| 导数(PNG) |
x^prime |
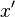 |
| 导数(错误) |
xprime |
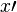 |
| 导数点 |
dot{x} |
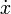 |
ddot{y} |
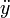 |
|
| 向量 |
vec{c} |
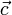 |
overleftarrow{a b} |
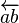 |
|
overrightarrow{c d} |
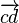 |
|
widehat{e f g} |
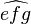 |
|
| 上弧(注: 正确应该用 overarc, 但在这里行不通。要用建议的语法作为解决办法) |
overset{frown} {AB} |
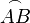 |
| 上划线 |
overline{h i j} |
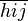 |
| 下划线 |
underline{k l m} |
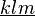 |
| 上括号 |
overbrace{1+2+cdots+100} |
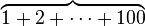 |
begin{matrix} 5050 overbrace{ 1+2+cdots+100 }end{matrix} |
 |
|
| 下括号 |
underbrace{a+b+cdots+z} |
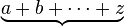 |
begin{matrix} underbrace{ a+b+cdots+z } 26end{matrix} |
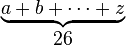 |
|
| 求和 |
sum_{k=1}^N k^2 |
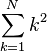 |
begin{matrix} sum_{k=1}^N k^2 end{matrix} |
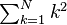 |
|
| 求积 |
prod_{i=1}^N x_i |
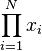 |
begin{matrix} prod_{i=1}^N x_i end{matrix} |
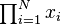 |
|
| 上积 |
coprod_{i=1}^N x_i |
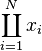 |
begin{matrix} coprod_{i=1}^N x_iend{matrix} |
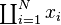 |
|
| 极限 |
lim_{n to infty}x_n |
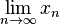 |
begin{matrix} lim_{n to infty}x_nend{matrix} |
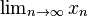 |
|
| 积分 |
int_{-N}^{N} e^x, dx |
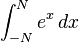 |
begin{matrix} int_{-N}^{N} e^x, dxend{matrix} |
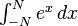 |
|
| 双重积分 |
iint_{D}^{W} , dx,dy |
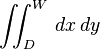 |
| 三重积分 |
iiint_{E}^{V} , dx,dy,dz |
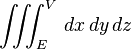 |
| 四重积分 |
iiiint_{F}^{U} , dx,dy,dz,dt |
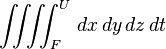 |
| 闭合的曲线、曲面积分 |
oint_{C} x^3, dx + 4y^2, dy |
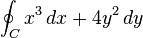 |
| 交集 |
bigcap_1^{n} p |
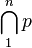 |
| 并集 |
bigcup_1^{k} p |
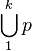 |
字体
斜体小写希腊字母一般用于在方程中显示变量。
| 正体希腊字母 |
|
|
|
| 特征 |
语法 |
效果 |
注释/外部链接 |
| 大写字母 |
Alpha Beta Gamma Delta Epsilon Zeta EtaTheta |
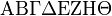 |
ΑΒ Γ ΔΕ Ζ ΗΘ |
Iota Kappa Lambda Mu Nu Xi Omicron Pi |
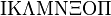 |
ΙΚ Λ ΜΝ Ξ ΟΠ |
|
Rho Sigma Tau Upsilon Phi Chi PsiOmega |
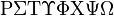 |
ΡΣ Τ ΥΦ Χ ΨΩ |
|
| 小写字母 |
alpha beta gamma delta epsilon zeta etatheta |
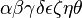 |
|
iota kappavarkappa lambda mu nu xi omicronpi |
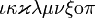 |
|
|
rho sigma tau upsilon phi chi psiomega |
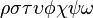 |
|
|
| 异体字母 |
Epsilonepsilonvarepsilon |
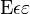 |
|
Thetathetavartheta |
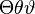 |
|
|
Kappakappavarkappa |
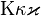 |
|
|
Pipivarpi |
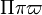 |
|
|
Rhorhovarrho |
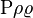 |
|
|
Sigmasigmavarsigma |
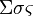 |
|
|
Phiphivarphi |
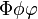 |
|
|
| 已停用字母 |
digamma |
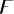 |
Ϝ[1] |
| 粗体希腊字母 |
|
|
| 特征 |
语法 |
效果 |
| 大写字母 |
boldsymbol{Alpha Beta Gamma Delta Epsilon ZetaEta Theta} |
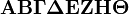 |
boldsymbol{Iota Kappa Lambda Mu Nu Xi OmicronPi} |
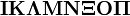 |
|
boldsymbol{Rho Sigma Tau Upsilon Phi Chi PsiOmega} |
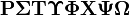 |
|
| 小写字母 |
boldsymbol{alpha beta gamma delta epsilon zetaeta theta} |
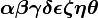 |
boldsymbol{iota kappa lambda mu nu xi omicronpi} |
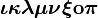 |
|
boldsymbol{rho sigma tau upsilon phi chi psiomega} |
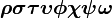 |
|
| 异体字母 |
boldsymbol{Epsilonepsilonvarepsilon} |
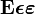 |
boldsymbol{Thetathetavartheta} |
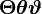 |
|
boldsymbol{Kappakappavarkappa} |
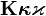 |
|
boldsymbol{Pipivarpi} |
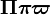 |
|
boldsymbol{Rhorhovarrho} |
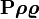 |
|
boldsymbol{Sigmasigmavarsigma} |
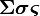 |
|
boldsymbol{Phiphivarphi} |
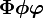 |
|
| 已停用字母 |
boldsymbol{digamma} |
|
黑板粗体
- 语法
mathbb{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
- 效果
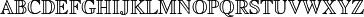
黑板粗体(Blackboardbold)一般用于表示数学和物理学中的向量或集合的符号。 备注:
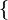 花括号
花括号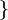 中只有使用大写拉丁字母才能正常显示,使用小写字母或数字会得到其他符号。
中只有使用大写拉丁字母才能正常显示,使用小写字母或数字会得到其他符号。
正粗体
- 语法
mathbf{012…abc…ABC…}
- 效果
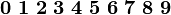
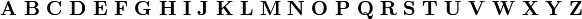
- 备注花括号{}内只能使用拉丁字母和数字,不能使用希腊字母如alpha等。斜粗体
- 语法
boldsymbol{012…abc…ABC…alpha betagamma…}
- 效果
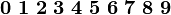
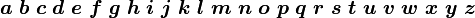
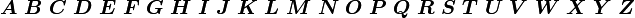
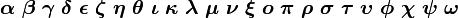
- 备注使用
boldsymbol{}可以加粗所有合法的符号。
斜体数字
- 语法
mathit{0123456789}
- 效果
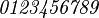
罗马体
- 语法
mathrm{012…abc…ABC…}或mbox{}或operatorname{}
- 效果
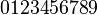
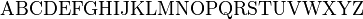
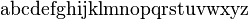
- 备注罗马体可以使用数字和拉丁字母。
哥特体
- 语法
mathfrak{012…abc…ABC…}
- 效果
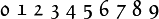
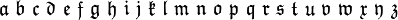
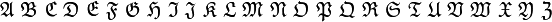
- 备注哥特体可以使用数字和拉丁字母。
手写体
- 语法
mathcal{ABC…}
- 效果
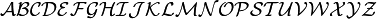
- 备注手写体仅对大写拉丁字母有效。
希伯来字母
- 语法
alephbethgimeldaleth
- 效果
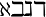
括号
| 功能 |
语法 |
显示 |
| 不好看 |
( frac{1}{2} ) |
 |
| 好看了 |
left( frac{1}{2} right) |
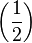 |
您可以使用 left 和 right 来显示不同的括号:

备注:
- 可以使用
big, Big, bigg, Bigg 控制括号的大小,比如代码
Bigg ( bigg [ Big {biglangle left | | frac{a}{b} | right | big rangleBig}bigg ] Bigg )
显示︰
Bigg ( bigg [ Big {biglangle left | | frac{a}{b} | right | big rangleBig}bigg ] Bigg )
空格
注意TEX能够自动处理大多数的空格,但是您有时候需要自己来控制。
| 功能 |
语法 |
显示 |
宽度 |
| 2个quad空格 |
alphaqquadbeta |
 |
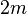 |
| quad空格 |
alphaquadbeta |
 |
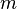 |
| 大空格 |
alpha beta |
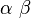 |
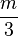 |
| 中等空格 |
alpha;beta |
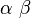 |
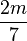 |
| 小空格 |
alpha,beta |
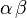 |
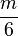 |
| 没有空格 |
alphabeta |
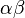 |
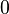 |
| 紧贴 |
alpha!beta |
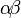 |
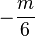 |
颜色
- 语法
- 字体颜色︰
{color{色调}表达式}
- 背景颜色︰
{pagecolor{色调}表达式}
*注︰输入时第一个字母必需以大写输入,如color{OliveGreen}。
{color{Blue}x^2}+{color{Brown}2x} -{color{OliveGreen}1}
$${color{Blue}x^2}+{color{Brown}2x} -{color{OliveGreen}1}$$
- ```latex
x_{color{Maroon}1,2}=frac{-bpmsqrt{{color{Maroon}b^2-4ac}}}{2a}
$$x_{color{Maroon}1,2}=frac{-bpmsqrt{{color{Maroon}b^2-4ac}}}{2a}$$
颜色小型数学公式
当要把分数等公式放进文字中的时候,我们需要使用小型的数学公式。
- 苹果原产于欧洲和中亚细亚。哈萨克的阿拉木图与新疆阿力麻里有苹果城的美誉。中国古代的林檎、柰、花红等水果被认为是中国土生苹果品种或与苹果相似的水果。苹果在中国的栽培记录可以追溯至西汉时期,汉武帝时,10的
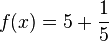 是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。
是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。 并不好看。
并不好看。
- 苹果原产于欧洲和中亚细亚。哈萨克的阿拉木图与新疆阿力麻里有苹果城的美誉。中国古代的林檎、柰、花红等水果被认为是中国土生苹果品种或与苹果相似的水果。苹果在中国的栽培记录可以追溯至西汉时期,汉武帝时,10的
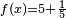 是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。
是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。 好看些了。
好看些了。
可以使用
begin{smallmatrix}...end{smallmatrix}
或直接使用 模板。
{{Smallmath|f= f(x)=5+frac{1}{5} }}
强制使用PNG
假设我们现在需要一个PNG图的数学公式。
- 若输入
2x=1 的话:
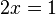
这并不是我们想要的。
- 若你需要强制输出一个PNG图的数学公式的话,你可于公式的最后加上
, (小空格,但于公式的最后是不会显示出来)。若输入 2x=1 ,的话:2x=1,
是以PNG图输出的。你也可以使用 ,!,这个亦能强制使用PNG图像。
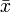
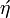
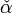
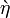
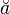
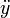
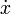
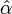
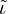
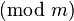
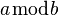

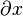
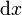
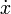
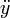
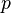
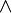
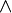
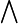
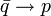
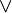

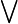

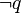
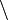
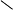
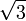
![pagecolor{White}sqrt[n]{3}](/wp-content/uploads/replace/21cb8585a0a0b036ee2109bb1d68eb1e.png)
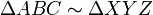
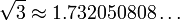
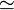
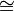
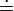
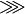
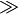
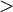
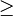
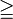

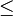
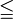
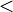
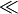
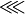
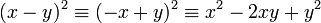
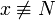
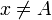
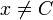
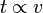
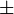
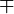
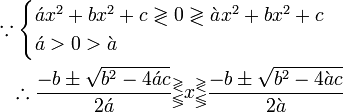
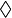

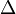
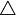
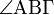






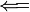
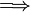
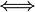
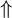
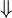
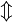
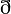
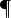
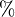
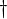
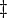
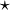
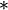
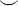

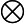
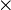

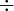





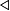
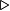
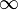
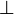
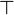
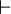
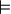
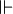
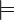
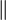
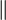

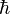
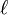
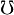
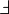
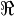
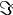
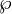
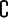
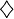
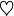

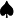
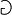
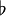
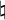
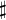
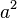
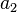
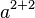
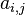
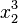
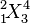
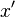
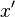
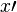
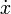
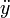
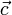
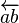
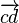
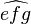
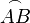
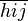
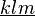
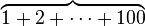
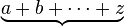
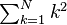
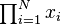
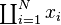
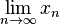
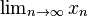
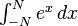
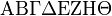
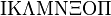
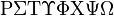
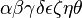
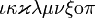
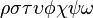
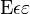
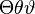
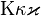
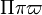
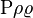
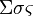
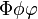
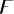


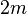

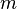
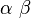
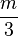
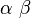
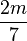
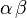
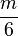
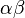
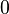
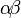
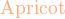
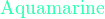

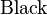
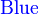
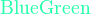
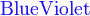
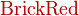
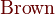

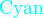
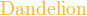

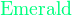
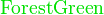
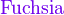
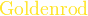
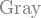
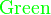
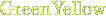
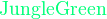
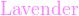
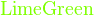
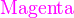
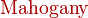
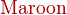
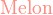
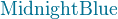
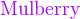
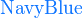
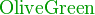
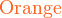
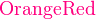
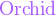
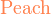
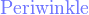

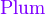
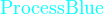
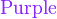
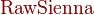


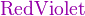
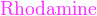
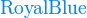
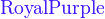
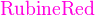
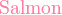
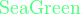
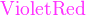
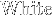
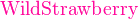
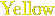
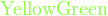
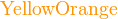
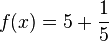 是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。
是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。 并不好看。
并不好看。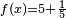 是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。
是2。上林苑中曾栽培林檎和柰,当时多用于薰香衣裳等,亦有置于床头当香熏或置于衣服初作为香囊,总之一般不食用。但也有看法认为,林檎和柰是现在的沙果,曾被误认为苹果,真正意义上的苹果是元朝时期从中亚地区传入中国,当时只有在宫廷才可享用。 好看些了。
好看些了。